拉格朗日方程

拉格朗日方程，因约瑟夫·路易斯·拉格朗日而命名，是拉格朗日力学的主要方程，可以用来描述物体的运动，特别适用于理论物理的研究。拉格朗日方程的功能相等于牛顿力学中的牛顿第二定律。

本文将给出拉格朗日方程的推导过程和分析力学的一些基础知识，还有一些相关介绍。

引言

在介绍拉格朗日方程之前，我们先简单介绍一下分析力学这门学科：

分析力学是理论力学的一个分支，它通过用广义坐标为描述质点系的变数，运用数学分析的方法，研究宏观现象中的力学问题。分析力学是独立于牛顿力学的描述力学世界的体系。分析力学的基本原理同牛顿运动三定律之间可以互相推出。

简单来说，分析力学就是将经典力学用更加数学化的方式来描述。它舍去了牛顿力学用的几何语言，使用广义坐标和变分法来代替，达到了牛顿的经典力学同样的效果，并且使得很多在牛顿力学里复杂的问题被简化。

而且分析力学的很多方法和结论都推广到量子力学和动力学系统之中，这使得分析力学具有很大的重要性。

拉格朗日方程

①拉格朗日函数

首先要知道，确定一个 N 个质点力学系统的位置，需要的是 3N 个坐标，这是因为在三维空间里，每确定一个点总是需要 3 个参数。并且一般把确定系统所需的参量个数称为系统的自由度，比如需要 3N 个参量就说自由度是 3N 。

然而可以发现，这些参数不一定需要是质点的笛卡尔坐标的三个分量，例如在球坐标和柱坐标系里面需要的参数就不一样。因此，对于一个力学系统，我们就把描述它的参量称为广义坐标 q ,而广义坐标的关于时间的导数就称为广义速度\dot q，这样就很自然地将一般笛卡尔坐标下的坐标和速度推广成了广义坐标和广义速度。

显然，在经典力学中，我们只要知道所有质点的广义坐标 q_i 和广义速度\dot q_i，原则上就可以预测接下来的系统的运动。因此每一个力学系统都由一个确定的函数 L 来表征，这个函数就依赖于系统中所有质点的广义坐标 q_i 和广义速度\dot q_i，并且因为系统随时间而发展，所以还需要一个时间变量 t 来描述这个函数在不同时间的值。

也就是说函数 L 的自变量是所有质点的广义坐标 q_i ，广义速度\dot q_i和时间 t 。

即一个 s 个自由度的系统就可以完全用函数L(q_1,q_2,\cdots,q_s,\dot q_1,\dot q_2,\cdots,\dot q_s,t)来描述，这个函数就叫做拉格朗日函数，一般简记为L(q,\dot q,t)。

②最小用量原理

最小作用量原理(或者叫哈密顿原理)就是说当系统从 t_1 变化到 t_2 时，系统的变化必须使得哈密顿量 S 取极值，其中哈密顿量为\[S = \int_{{t_1}}^{{t_2}} {L(q,\dot q,t)}dt \]，。也就是说系统的拉格朗日函数在从t_1 变化到 t_2这个过程中要使得 S 取极值。虽然叫做最小作用量原理，但实际上是取极值而不是最小值。

最小作用量原理在力学中是作为公理存在的，所以也没法推导，关于最小作用量可参考：

③拉格朗日方程推导

现在我们就可以通过最小作用量原理来推导出物体运动所要满足的运动方程了，这个方程也就是拉格朗日方程。

下面简单推导一下：

首先，如果一个函数 q(t) 使得哈密顿量 S 取极值，因此给这个函数加上一个很小的扰动函数 \delta q(t) 几乎不会使得作用量产生变化，因为在极值处变化率为零。

其中的函数\delta q(t)在整个时间间隔中都是一个很小值，并且在时间的开始和结束处值都必须为零，即 \delta q(t_1)=\delta q(t_2)=0 。

也就是说 \int_{{t_1}}^{{t_2}} L(\dot q + \delta \dot q,q + \delta q,t)dt- \int_{{t_1}}^{{t_2}}L(\dot q,q,t)dt=0

即\int_{{t_1}}^{{t_2}} {[L(\dot q + \delta \dot q,q + \delta q,t)} - L(\dot q,q,t)]dt =0

然后展开取一阶量就可以得到\int_{{t_1}}^{{t_2}} {(\frac{{\partial L}}{{\partial \dot q}}} \delta \dot q + \frac{{\partial L}}{{\partial q}}\delta q )dt=0，

又因为 \delta \dot q=\frac{d}{dt}\delta q， 然后再把第二项部分积分，

就可以得到\frac{\partial L}{\partial \dot q}\delta q\bigg|_{t_1}^{t_2}+ \int_{{t_1}}^{{t_2}} { (\frac{{\partial L}}{{\partial q}} - \frac{d}{{dt}}\frac{{\partial L}}{{\partial \dot q}})\delta q\;\ dt} =0

因为\delta q(t_1)=\delta q(t_2)=0，所以上式中第一项为零，

所以 \int_{{t_1}}^{{t_2}} { (\frac{{\partial L}}{{\partial q}} - \frac{d}{{dt}}\frac{{\partial L}}{{\partial \dot q}})\delta q\;\ dt} =0 \;\ ，

现在又因为 \delta q(t) 是任意的，所以\[{\frac{{\partial L}}{{\partial q}} - \frac{d}{{dt}}\frac{{\partial L}}{{\partial \dot q}}} = 0\] 。

在多个广义坐标时候类似地可以得到：

\int_{{t_1}}^{{t_2}} {\sum\limits_i {\delta {q_i}(\frac{{\partial L}}{{\partial {q_i}}} - \frac{d}{{dt}}\frac{{\partial L}}{{\partial {{\dot q}_i}}})} dt} =0，

即\frac{{\partial L}}{{\partial {q_i}}} - \frac{d}{{dt}}\frac{{\partial L}}{{\partial {{\dot q}_i}}}= 0 \;\ (i=1,2,\cdots,s)，这就是拉格朗日方程。

也就是说，如果我们知道了一个系统的拉格朗日函数，把它代入这个方程就可以得到这个系统的运动方程。

一般来说，通过伽利略相对性原理可得到质点系的拉格朗日函数 L=T-U ,其中 T 为质点系得动能， U 为质点系的势能。

因此为了计算力学系统的运动方程，我们只需要写出系统的拉格朗日函数关于广义坐标和广义动量的表达式，然后代入拉格朗日方程就可以得到运动方程了，这就是为什么分析力学不需要涉及几何，而只需要代数运算就能解决力学问题。

这就是为什么拉格朗日的分析力学这本书一张图都没有。。。

拉格朗日《分析力学》这本著作是在1788年写成的。全书根据一个虚位移原理，用严格的数学分析方法来处理所有的力学问。全书自始至终没有用到过一张图，拉格朗日本人曾经以此而感到非常满意和十分骄傲。

然而不得不提的是，历史上的拉格朗日方程实际上是从达朗贝尔原理得到的，也就是直接从牛顿力学公式推广得到的，而哈密顿原理才是从拉格朗日方程总结出来的，本文的推导是从哈密顿原理推出拉格朗日方程。

想看从牛顿力学推导的可以参考下文：

拉格朗日

拉格朗日父亲是法国陆军骑兵里的一名军官，后由于经商破产，家道中落。据拉格朗日本人回忆，如果幼年时家境富裕，他也就不会作数学研究了，因为父亲一心想把他培养成为一名律师。拉格朗日个人却对法律毫无兴趣。

拉格朗日科学研究所涉及的领域极其广泛。他在数学上最突出的贡献是使数学分析与几何与力学脱离开来，使数学的独立性更为清楚，从此数学不再仅仅是其他学科的工具。

拉格朗日总结了18世纪的数学成果，同时又为19世纪的数学研究开辟了道路，堪称法国最杰出的数学大师。同时，他的关于月球运动（三体问题）、行星运动、轨道计算、两个不动中心问题、流体力学等方面的成果，在使天文学力学化、力学分析化上，也起到了历史性的作用，促进了力学和天体力学的进一步发展，成为这些领域的开创性或奠基性研究。

更多内容请参考百度百科：

发展

分析力学的发展历史：

1788年：

拉格朗日出版的《分析力学》是世界上最早的一本分析力学的著作。分析力学是建立在虚功原理和达朗贝尔原理的基础上。两者结合，可得到动力学普遍方程，从而导出分析力学各种系统的动力方程。

1760年：

拉格朗日用这两个原理和理想约束结合，得到了动力学的普遍方程，几乎所有的分析力学的动力学方程都是从这个方程直接或间接导出的。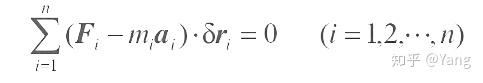

1834年：

哈密顿推得用广义坐标和广义动量联合表示的动力学方程，称为正则方程。哈密顿体系在多维空间中，可用代表一个系统的点的路径积分的变分原理研究完整系统的力学问题。

1861年：

从有人推导出球在水平面上作无滑动的滚动方程开始，到1899年阿佩尔在《理性力学》中提出阿佩尔方程为止，基本上已完成了线性非完整约束的理论。

20世纪：

对非线性、不定常、变质量等力学系统作了进一步研究，对于运动的稳定性问题作了广泛的研究。

本文内容参考：朗道 力学

注：文章图片来源于百度