怎么理解流体力学中的欧拉描述和拉格朗日描述？

流体力学中的Euler描述和Lagrange描述

南京理工大学 魏峰

（1）Euler描述

Euler描述是一种场描述，可以这么理解，如果你是观察者，你的视线始终盯在某一个位置或是某几个位置，但是即使被观察的物体的空间位置发生移动，你的视线始终不能够移动。Euler描述区别于Lagrange描述的地方在于Euler描述是观察空间位置，而Lagrange描述是观察具体的物体或是质点。基于这种特点，欧拉描述可以用以下这种数学形式来表达：

假设被观察的空间位置为点P，它的坐标为(x,y,z)（上文已经说明，被观察的空间位置可以有很多个乃至无限多个，点P也是一个动点，他的位置可以是被研究空间上任意一点，所以坐标(x,y,z)也是变量）。与空间位置对应的物理量都可以相应的表示出来，但是由于随着时间的变化，同一个空间位置的某一物理量可能也会发生变化，所以变量必须还要包含时间t。

Example: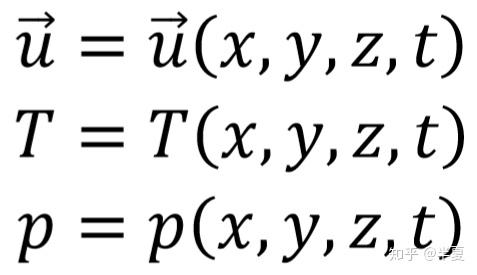

接下来表示Euler描述下的加速度。由于x,y,z,t均为u 的变量，所以加速度为：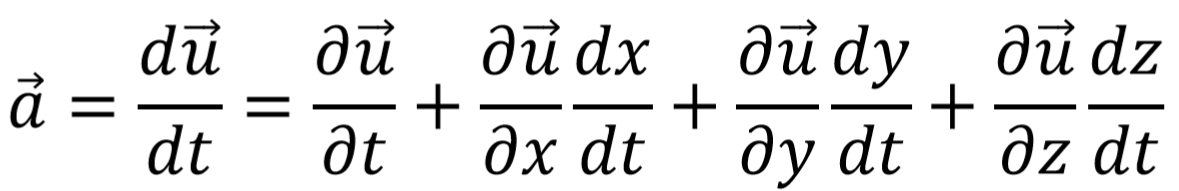

如果令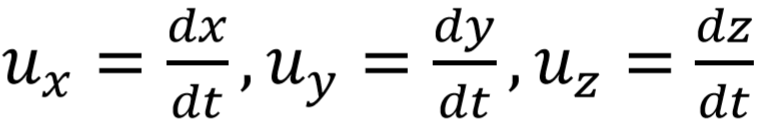

那么：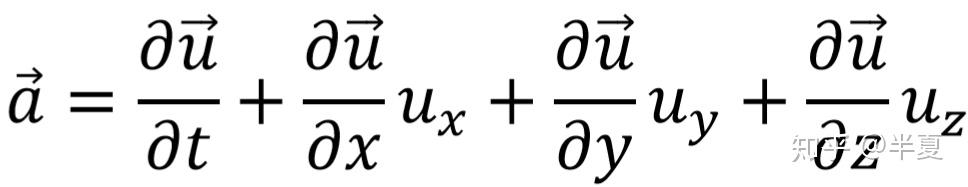

有关于速度和加速度的问题文章的最后将把Euler描述与Lagrange描述进行对比说明为什么要这样求解。

（2）Lagrange描述

区别于Euler描述，Lagrange描述是观察具体的质点，如果你是观察者，你的视线将跟随着某个或者很多个质点一起运动，并且视线永远不能离开你要观察的质点。基于这种观察方法，只需要在一开始确定你要观察的质点是哪一个或者哪一些，那么今后该质点的状态实时的都是可以知道的，同样使用坐标(x,y,z)去表示质点的位置，如果确定了要观察的质点，那么(x,y,z)只是时间t的函数，但是如果没有确定要观察的质点，那么在同一时刻对不同的质点来说，他们的坐标也是不同的。那么如何确定不同的质点呢？上文已经说过，使用质点在初始时刻的位置来区分不同的质点，所以还需要引入质点初始时刻坐标这个变量，用(a,b,c)表示。如果对这个过程的理解还是比较模糊，可以这样考虑，将时间t固定，那么质点都停止在画面上（速度还是有的），此时根据初始时刻的坐标去寻找不的质点，就能很明显的发现(x,y,z)是(a,b,c)的函数。

如果观察一个质点Q（注意这里Q的空间位置是不固定的），那么他的坐标(x,y,z)都可以写成时间t的函数，如果将这个质点Q看成是一个“动点”（注意这里的动点不是一般意义上的动点，一般意义上的动点只是允许空间位置的移动，而这里的动点是指允许该点代表不同的质点，即允许其初始位置的改变），所以坐标(x,y,z)也是(a,b,c)的函数。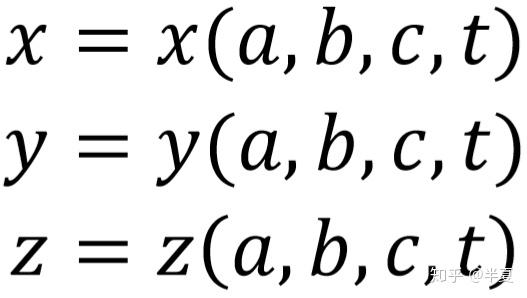

接下来表示Lagrange描述下的速度。由于Lagrange描述是直接跟踪质点，所以其速度可以表示为：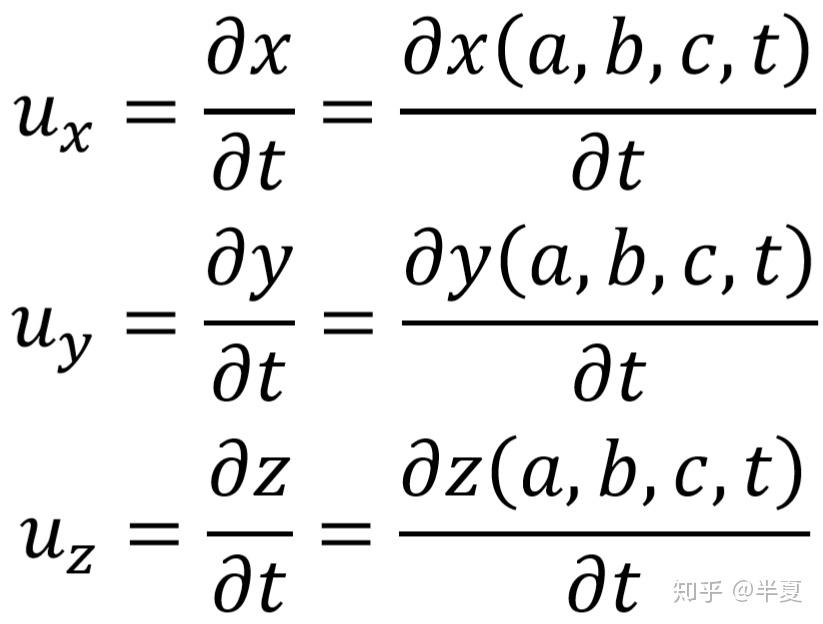

接下来表示Lagrange描述下的加速度。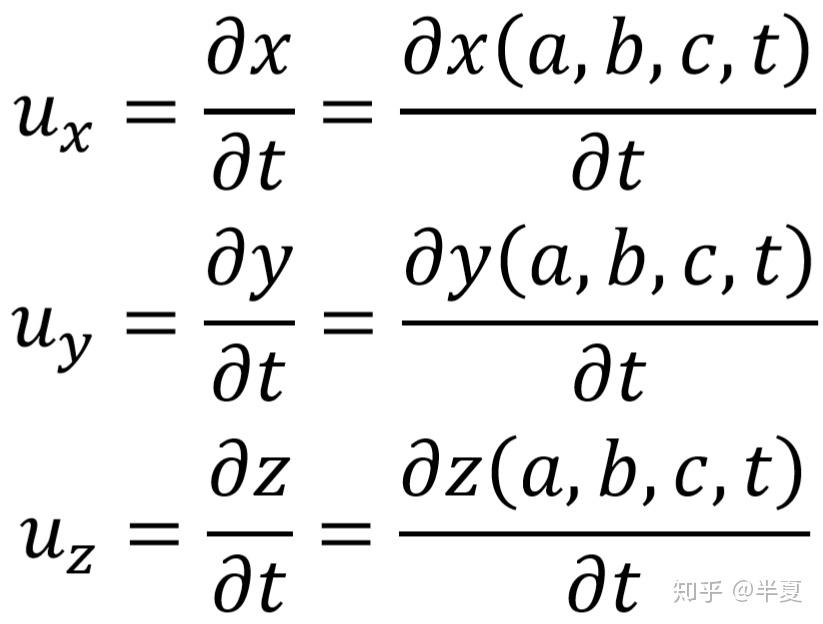

1.为什么Euler描述中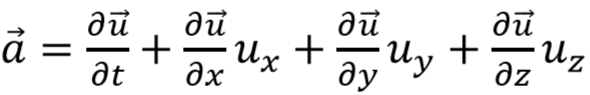

而Lagrange描述中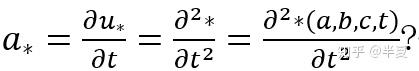

答：从数学角度来说，Lagrange描述中(a,b,c)不是时间t的变量，所以其对t的全导数与对t的偏导数是一样的。而Euler描述中(x,y,z)本身就是t的变量。从物理的角度来说，Euler描述由于是视线固定在具体的空间位置上，而加速度指的是具体质点的加速度。假定观察的空间位置为点P,在t时刻质点H在点P的临近位置上，在t+△t时刻质点H移动到点P位置。在△t时间内，质点H的加速度本身就会发生改变，然后还会有空间位置移动带来的加速度的变化，因为我们描述速度是描述的空间点P的速度，而不是质点H的速度。更加严谨的证明过程由于小编的数学知识有限所以无法给出。

2.在Euler描述中x/t表示什么？

答：无意义。