图论与线性代数--用矩阵性质了解图性质-拉普拉斯矩阵

图形是一种难以置信的多功能结构，因为它可以模拟一切事物，从计算机科学的现代性和地理的复杂性，到语言关系的复杂性和化学结构的普遍性。将此类图表示为矩阵只会增强此建模的计算方面。最终，这需要线性代数。

本文探讨了图论及其相关矩阵表示与线性代数中矩阵性质之间的关系。它不仅研究了图的邻接矩阵，而且还研究了关联矩阵、路矩阵、距离矩阵和拉普拉斯矩阵中更有趣的例子。研究包括各种图的矩阵表示的实用性，包括不连通图、完全图和树。为了实现这一目标，本文提出了一些关于图的矩阵表示的最有趣的定理，并将这些定理与图论本身的问题联系起来。

最后，本文确定了特殊类图（即完全图和无环图（树）的某些独特性质，以及它们在图论中的特殊性如何反映在它们的矩阵性质中。同样，这种分析使用线性代数。许多这样的定理为这些类提出了特殊的关系，其中一些已经被研究过，而另一些仍有待完全理解。

1. 基础图论
   图论研究与图相关的结构、性质和算法。图有许多等价表示；特别是一种表示法被广泛用作主要定义，本文也将采用这一标准。
   图（表示为G）定义为由两个不同集合组成的有序对：
1. 一组顶点，表示为V（G）
2. 一组边，表示为E（G）
   |1.2.1|1.2.1|1.2.1|1.2.1
   图G的序指V（G），图G的大小指E（G）。换句话说，顺序是指顶点的数量，大小是指边的数量。
   为了对这些图进行计算，我们使用矩阵作为一种非常有价值的替代表示。这种表示包括关联矩阵、邻接矩阵、距离矩阵和拉普拉斯矩阵。

1. 邻接矩阵
2. 定义
   对于n阶图G，图G的邻接矩阵a（G）是n×n矩阵，其（i，j）-th项确定如下：Aij==1, if
   顶点vi与顶点vj相邻0，否则为（1）
   邻接矩阵不仅封装了图的结构和关系，而且为计算机的存储和访问提供了一种有效的方法。因此，邻接矩阵是表示图的最常用的方法之一。
3. A的距离和幂
   图G的顶点vi和vj之间的距离，用两个顶点之间的最小长度的路径定义。例如，以图中的图形为例。如图所示，顶点v6和v8之间有两条长度为4的路径。12
   图的邻接矩阵提供了一种通过计算矩阵的幂来计算这些路径的方法。
   定理2.1。设G是邻接矩阵为a的图，k是正整数。然后矩阵幂Ak给出矩阵，其中Aij计算顶点vi和vj之间长度为k的路径数。
   例如，返回图中所示的图形。方程描述了图的邻接矩阵A（G）及其四次方。22
   

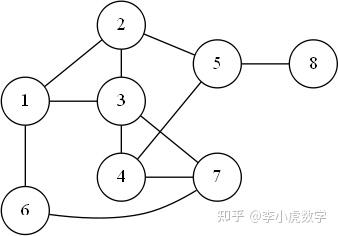
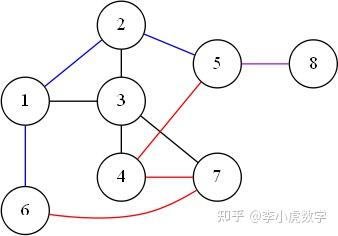
图1：顺序图8

图2：顶点6和8之间的2条路径的描述

A（G） =0 1 0 1 0 0 1 A（G）=10416415410 0

（2）
1 0 0 0 0 1 0
0 0 1 1 0 1 0 0
0 0 0 0 1 0 0 0
16 11 13 11 10 417 2
正如预期的那样，A4（G）的（6,8）-条目通过对称性计算顶点v6和v8之间的两条路径，对于（8,6）-条目也是如此。虽然这个结果提供了一个有用的方法来计算图中顶点之间的路径数，但它可以扩展到一个类似的有趣的逻辑推论。
推论2.1。设G是邻接矩阵为a的图，k是正整数。那么sum Sn定义为
Sn = A + A2 + ... + Ak(3)
是n x n矩阵，其（i，j）-条目统计顶点vi和vj之间长度为k或更小的路径数。
在此，矩阵再次提供用于识别和组织图的属性的计算有用的工具。

1. 特征值与完全图

n阶完全图G（Kn）在每对顶点之间都有一条边。例如，K5如图所示。3

n=p+q阶完全二部图G由两个集合U，VE（G）组成，其中U的每个顶点与V的每个顶点相邻，且同一集合中没有两个顶点相邻。例如，图中描绘了K2,3。4

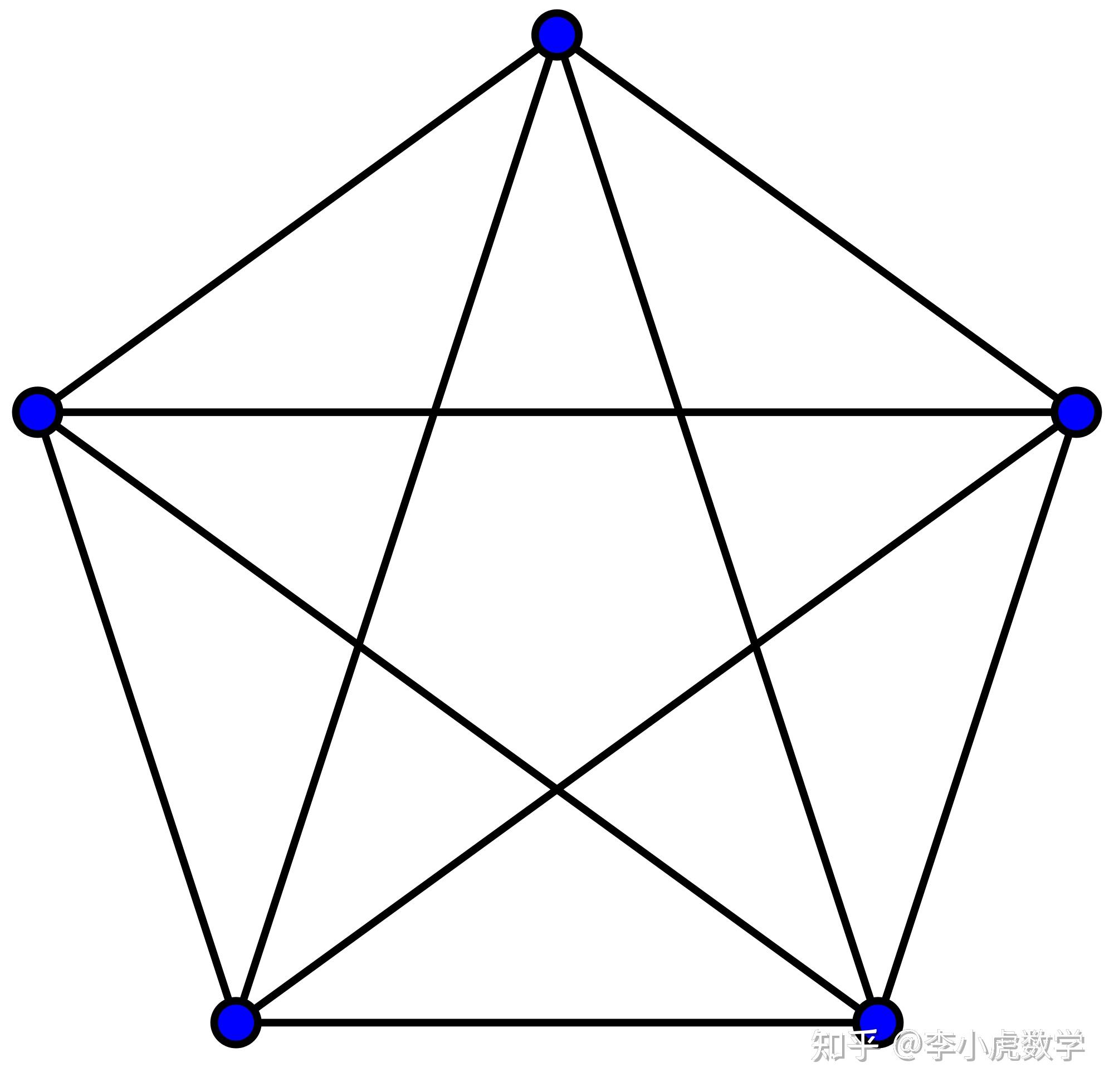
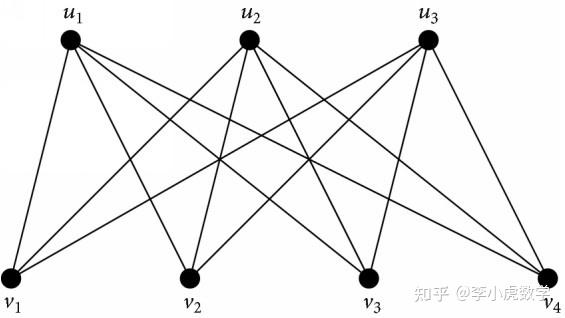
图3：完全图K5图4：完全二部图K3,4

图G的特征值是其邻接矩阵的特征值。在完全图（包括完全图和完全二部图）的情况下，出现了一些有趣的模式。

定理2.2。对于任意正整数n，Kn的特征值为重数为1的n1和重数为n-1的1。对于任意正整数p，q，K的特征值分别为√pq、-√pq和重数为p+q2的0。

虽然这个结果本身很有趣，但这个定理可以用来将图论的基本结果与线性代数的基本结果交织在一起。

在图论中，从n阶完全图中删除任何顶点（及其关联边）将得到n1阶完全图。结合这一事实和上述结果，这意味着A（Kn）的每个nk+1平方子矩阵，1≤k≤n具有重数k的特征值1和重数1的特征值nk+1。值得注意的是，这产生了a（Kn）的子矩阵特征值的自然界：

1≤λi≤n，1≤i≤n

这一结果也出现在线性代数中，作为对称矩阵的一般性质：所有对称矩阵的交错特征值出现，线性代数等价于图论中的这一自然结果。

1. 关联矩阵
2. 定义
   对于n阶m的图G，G的关联矩阵Q（G）表示为n×m矩阵，其（i，j）-th项确定如下：
   Qij=1, if 顶点vi与边ej关联0，否则为（4）
   虽然关联矩阵在计算上不如邻接矩阵有用，但它们使用线性代数保留了某些有趣的性质。
3. 发病率和等级
   首先，观察：Q（G）的列和都是零，因此Q（G）的行是线性相关的，因为由所有1组成的向量跨越Q的零空间。因此，任何图的关联矩阵Q的秩必须小于n阶。然而，对于任何图G，只有一列是其他列的线性组合：
   引理3.1。如果G是n个顶点上的连通图，则秩Q（G）=n1。
   然而，这个引理只适用于连通图，其中任何一对顶点之间都存在一条路径。不连通图是指至少有一对顶点之间没有路径的图。这说明了并非所有顶点都需要位于图的同一部分的直观想法，如图中的示例所示。5
   

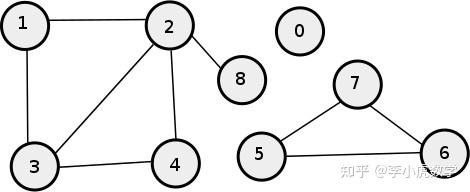
图5：9阶断开连接图
图G的每个连通子段称为分量G。对于连通图，只有一个分量。利用前面的引理，我们可以对任何图产生一个更一般的结果。
定理3.1。如果G是n个顶点上的图，并且有k个连通分量，则秩Q（G）=nk。
因此，关联矩阵捕获了图的另一个方面。邻接矩阵捕获图的密度并允许计算顶点之间的关系，而关联矩阵则说明边与顶点的关系，因此与属性（如组件）相关。

1. 路径矩阵与关联矩阵

设G是一个大小为m和u，v v（G）（即G的任意两个顶点u和v）的图。顶点u和v的路径矩阵–表示为P（u，v）-是q x m矩阵，其中q是u和v之间不同路径的数量，定义如下：

P（u，v）ij=1, if 边ej位于第i条路径vj中 ，否则为。（5）

换句话说，路径矩阵是为图G中的一对顶点定义的，其中

P（u，v）的行对应于从顶点u到顶点v的不同路径（例如，可以使用邻接矩阵Am（G）的m次方进行计数，如第节中所述）2.2

P（u，v）的列分别对应于图G中的一条边

令人难以置信的是，图的关联矩阵与其路径矩阵之间存在联系。

定理3.2。设G是n阶图，且至少有两个顶点u，v（G）。排列其关联矩阵Q（G）的列，使其与路径矩阵P（u，v）的列对齐。然后，

Q（G） *PT（u，v）（mod 2）=M，（6），其中M是两行u和v中的所有1，其余n-2行中的0的矩阵。

在此，关联矩阵再次封装边和顶点关系，而不仅仅是在邻接矩阵中发现的顶点关系。然而，最强大的矩阵表示之一尚未出现。

1. 拉普拉斯矩阵
2. 定义
   顶点vi的度数，表示为di，是顶点i相邻的其他顶点的总数。也就是说，每个顶点的阶数是从该顶点入射的边数。这为我们定义拉普拉斯矩阵提供了知识基础，乍一看，拉普拉斯矩阵似乎完全是任意的，但有许多令人难以置信的性质。图G的拉普拉斯矩阵，表示为L（G），是定义如下的n乘n矩阵：
   Lij =
   
   0，如果顶点vi与顶点vj不相邻
   1，如果顶点vi与顶点vj相邻
   di，如果i=j
   
   （7）
   负极
   因此，拉普拉斯矩阵的每个顶点沿其对角线的度数，如果两个顶点相邻，则为a1。否则，每个其他条目都由全零组成。
   如果我们定义D（G）是一个对角矩阵，它的条目是每个顶点的度，那么图G的拉普拉斯矩阵可以等价地定义为
   L（G） =D′（G）-A（G）（8）
   值得注意的是，拉普拉斯矩阵也可以用关联矩阵表示。将任意方向赋给图G–即，将固定的任意方向赋给每条边–G的拉普拉斯矩阵可以用有向表示的关联矩阵表示：
   L(G) = Q(G)Q(G)T(9)
   例如，以图中的基本图形为例：6
   

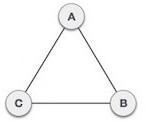
图6：拉普拉斯矩阵示例
该图的拉普拉斯矩阵，包括其与邻接矩阵和入射矩阵的关系，如等式所示：10
L（G）=
121 = 0 2 0 1 0 1 = 110 011
211
112

2 0 0
0 0 2

0 1 1
1 1 0

101

110
（10）

1. 负极
   矩阵树定理

图G的生成树是G的子图，即生成树是与G在同一顶点集上的树，它使用E（G）的某个子集，使得每个顶点至少与一条边相邻。可以想象，计算一个图G的所有生成子树可以很快成为一项艰巨的任务。然而，存在一个有效的解决方案，它利用拉普拉斯矩阵。

也就是说，图论中最有用、最优美的定理之一是矩阵树定理。

定理4.1（矩阵树定理）。设G是n阶图，则L（G）的任一元素的余因子等于G的生成树的个数。

也就是说，一个拉普拉斯矩阵的所有余因子都是相同的，并且共享值统计图G的生成树的数目！

11

返回到上面的例子。取三角形拉普拉斯矩阵的（2,3）-余因子：

C23= (1)2+3 21 = (1) (2 1) = 3(11)

它对应于图的3个生成树，如图所示。7

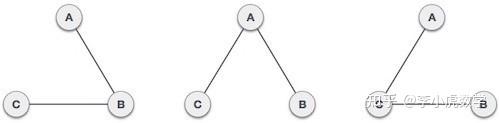
图7:K3的三个生成树

可以很容易地检查拉普拉斯矩阵的每一个其他辅因子产生相同的结果。

1. 距离矩阵
2. 定义
   对于n阶图G，图G的距离矩阵D（G）是n×n矩阵，其（i，j）-th项是顶点vi和vj之间的距离。自然地，这意味着D（G）是一个对称矩阵，其对角线完全由零组成。
3. 距离矩阵与树
   将距离矩阵应用于树时，出现了一个有趣的通用性：
   定理5.1。设T为n阶树，则D（T）的行列式为
   详细数据D（T）=（1）n1（n1）*2n2（12）
   ≥
   虽然这似乎是一个微不足道的结果，但它有着深刻的含义。首先，作为与线性代数的直接联系，由于n3阶树的行列式都是非零的，因此所有树的距离矩阵都是非奇异的。也就是说，树的所有距离矩阵都有一个逆矩阵
   第二，由于行列式只取决于矩阵的大小，而不取决于条目的位置，因此结果只取决于给定树的大小，而不依赖于它的结构或形状。也就是说，在n阶nn2树中，它们的每一个距离矩阵都具有相同的行列式。这表明了所有树之间潜在的相似性，这种相似性一直存在于关于树的无数其他结果中，并且猜想的多样性更大。
4. 拉普拉斯矩阵与距离的关系

最后，树的距离和拉普拉斯矩阵之间存在联系：

定理5.2。设T是一棵n阶树，具有拉普拉斯矩阵L和距离矩阵D

低密度脂蛋白=-2L

同样，树存在一种模式，这种模式在其他图中不存在，它出现在给定顺序的所有树中，而不管它们的结构或形状如何。它暗示了一个潜在的相似之处。

参考文献

1. 图矩阵，2010。[在线；访问日期：2017年3月16日]。http://compalg.inf.elte.hu/tony/Oktatas/TDK/决赛/Ch2010年ap%。PDF格式
2. R、 B.Bapat。图形和矩阵。印度斯坦图书局，新德里，印度。
3. Gary Chartrand和Ping Zhang。图论的第一门课。多佛出版社，波士顿，2012年。
4. 道格拉斯E恩斯利和J温斯顿克劳利。离散数学。John Wiley and Sons，Inc.，Hoboken，新泽西州，2006年。
5. Laszlo Lovasz。图的特征值，2007。[在线；2017年3月17日查阅]。http://www.cs.elte.hu/lovasz/egenvals-x.pdf
6. 达米尔·武基切维奇和伊万·古特曼。树中的拉普拉斯矩阵和距离矩阵，2004。[在线；2017年3月17日查阅]。http://elib.mi.sanu.ac.rs/files/journals/kjm/26/d003download.pdf