|
视频:https://space.bilibili.com/555233120 博文:https://www.zhihu.com/column/c_1531055529060831232 代码:https://gitee.com/yifanrensheng/deep_learning_for_cv 文章概述:主要介绍 CNN 网络发展,重点讲述了搭建 CNN 网络的组件:卷积层,池化层,激活层和全连接层。 1、CNN 简介卷积神经网络(Convolutional Neural Networks,CNN)属于神经网络的一个重要分支。应用于CV,NLP等的各个方面。 1 发展史
2 出现的原因1)传统神经网络参数巨大 VS CNN的参数共享机制 ① 参数更少
② 平移不变性:由于filter的参数共享,即使图片进行了一定的平移操作,我们照样可以识别出特征。因此,模型就更加稳健了。 2)局部感受野 局部范围内的像素之间联系较为紧密,而距离较远的像素则相关性较弱。因而,每个神经元其实没有必要对全局图像进行感知,只需要对局部进行感知,然后在更高层将局部的信息综合起来就得到了全局的信息。而且每一个区域都有自己的专属特征,我们不希望它受到其他区域的影响。 3 常见的结构一般而言,CNN主要由以下层构造而成:
2、卷积层1 卷积的理解CNN 中最为重要的部分,而卷积其实主要的就是用对应的卷积核(下图左侧黄色)在被卷积矩阵上(下图左侧绿色)移动做乘法和加法得到提取后的特征(如下图右侧)。 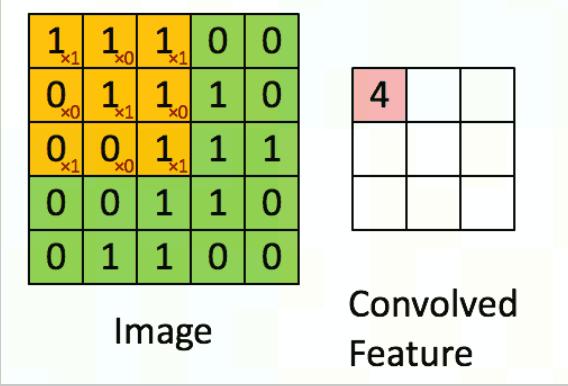 2 PyToch中的公式常用的卷积(Conv2d)在pytorch中对应的函数是: torch.nn.Conv2d(in_channels,out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)
以上很多参数会影响对应的输出特征大小。  【图片截取自pytorch官网】 注意:pytorch的图片载入tensor的顺序:[ Batch,Channel,Height,Width ] 实际应用中,dilation相对较少,因此特征图的边长公式一般可以简化如下: N=(WF+2P)/S+1 其中:
说明:当所得N为非整数时,我们采用向下取整(等于小于自己的最大整数)的方式进行。 3 卷积对通道的影响及计算1)通道影响 一般卷积过程如下图所示,其中:
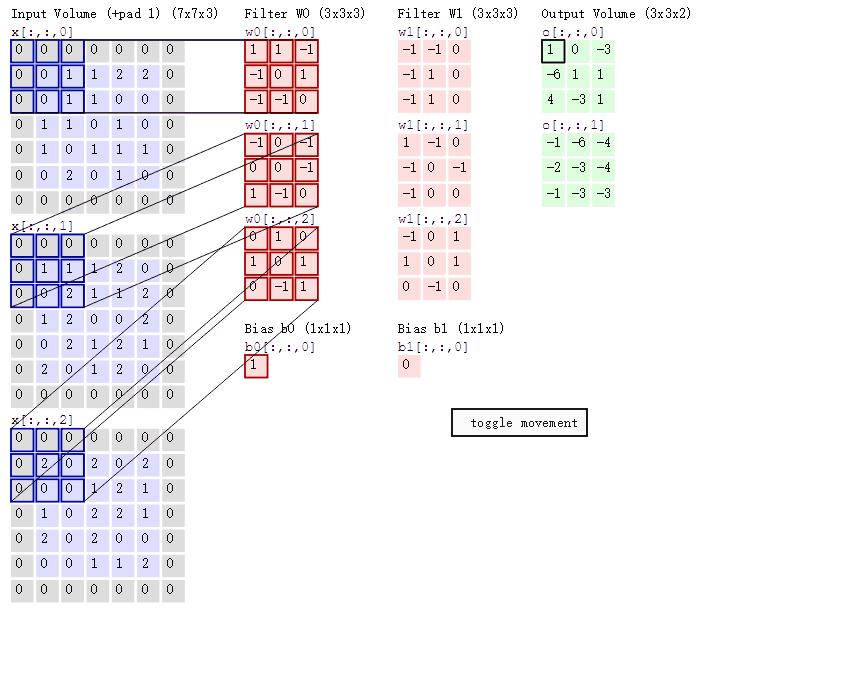 ① 对于输出宽度,再校验一次上述公式: \begin{aligned} &公式: N=(WF+2P)/S+1 \\ &本例:3 = (5-3 +2*1)/2 +1 \end{aligned} ② 对于最终的特征值的数量为2个,这个根据卷积核的组数决定的,也即中间红色部分是两列。若是想得到更多特征数量,可以增加卷积核的组数来控制。 2)训练中参数计算 假设卷积核大小为 n*m,输入时有C个通道(channels)/维度,而选用的"卷积核/filter"有K个,再加上1个bias,可以得到引进的参数有: \begin{aligned} &公式:(n*m*C+1)*k \\ &本例:(3*3*3+1)*2\\ \end{aligned} 3、池化层1 池化层的理解池化层不改变三维矩阵的深度,可以缩小矩阵的大小。池化操作可以认为是将一张分辨率高的图片转化为分辨率较低的图片。通过池化层,可以进一步缩小最后全连接层中节点的个数,从而到达减少整个神经网络参数的目的。池化层本身没有可以训练的参数。一般有三种池化策略:
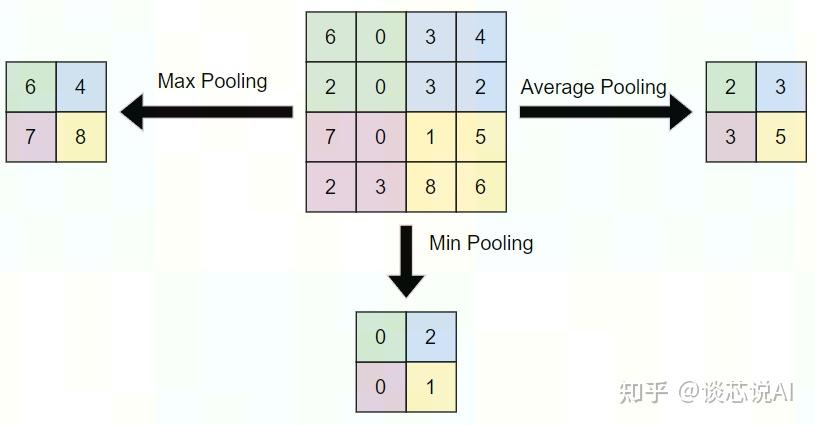 2 池化层计算公式1)PyTorch 接口和公式 torch.nn.MaxPool2d(kernel_size,stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
 【图片截取自 pytorch官网 】 实际应用中,dilation相对较少,因此特征图的边长公式一般可以简化如下: N=(WF+2P)/S+1 其中:
说明:当所得N为非整数时,默认采用向下取整(等于小于自己的最大整数)的方式进行。 2)一般经验
4、激活层激活函数(Activation Function),就是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。 激活函数的主要作用是提供网络的非线性建模能力。如果没有激活函数,那么该网络仅能够表达线性映射,此时即便有再多的隐藏层,其整个网络跟单层神经网络也是等价的。因此也可以认为,只有加入了激活函数之后,深度神经网络才具备了分层的非线性映射学习能力。 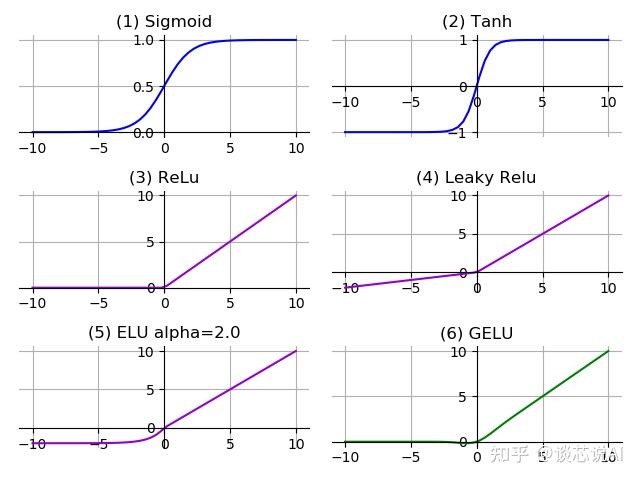 该图可用代码中的tools activate_test.py 运行得到。 1 SigmoidSigmoid函数也叫Logistic函数,用于隐层神经元输出,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。sigmoid是一个十分常见的激活函数,函数的表达式如下: \begin{aligned} & f(x) = \frac{1}{1+e^{-z}} \\ & f'(x) = f(x)(1-f(x)) \end{aligned} 优点:
缺点:
2 Tanh(双曲正切函数)它是完全可微分的,反对称,对称中心在原点。为了解决学习缓慢和/或梯度消失问题。 \begin{aligned} & f(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \\ & f'(x) = 1-f^2(x) \end{aligned} 优点:
缺点: 还是没有改变Sigmoid函数的最大问题——由于饱和性产生的梯度消失。 3 ReLU(Rectified linear unit) 修正线性单元\begin{aligned} & f(x)= max(0,x) \\ & f'(x) = \begin{cases} 0 , \quad & if \; x<0 \\ 1 , \quad & if \; x>0 \\ underfined , \quad & if \; x=0 \\ \end{cases} \end{aligned} 优点:
缺点:
4 Leaky ReLU经典(以及广泛使用的)ReLU 激活函数的变体,带泄露修正线性单元(Leaky ReLU)的输出对负值输入有很小的坡度。由于导数总是不为零,这能减少静默神经元的出现,允许基于梯度的学习(虽然会很慢)。 \begin{aligned} & f(x) = max(\alpha x, x) \\ & \\ & 其中: \\ & \alpha \; 一般取很小的数值,比如 0.01等\\ \end{aligned} 优点:
缺点:
5 ELUELU(Exponential Linear Unit) 的提出同样也是针对解决 ReLU负数部分存在的问题,由Djork等人提出,被证实有较高的噪声鲁棒性。ELU激活函数对 x 小于零的情况采用类似指数计算的方式进行输出。与 ReLU 相比,ELU 有负值,这会使激活的平均值接近零。均值激活接近于零可以使学习更快,因为它们使梯度更接近自然梯度。 函数表达式为 \begin{aligned} & f(x) = \begin{cases} \alpha (e^x -1), \quad & if \; x ≤ 0 \\ x , \quad & if \; x > 0 \\ \end{cases} \\ & f'(x) = \begin{cases} f(x) + \alpha, \quad & if \; x ≤ 0 \\ 1 , \quad & if \; x > 0 \\ \end{cases} & \\ &其中:\\ & \alpha \; 一般取1或2\\ \end{aligned} 优点:
缺点:
6 GELUGELU(Gaussian Error Linear Unit 高斯误差线性单元)是一个非初等函数形式的激活函数,是RELU的变种。由16年论文 Gaussian Error Linear Units (GELUs) 提出,随后被GPT-2、BERT、RoBERTa、ALBERT 等NLP模型所采用。因为gelu的非线性变化是一种符合预期的随机正则变换方式,公式如下: \mathrm{xP}(\mathrm{X} \leq \mathrm{x})= \mathrm{x} \int_{-\infty}^{\mathrm{x}} \frac{\mathrm{e}^{-\frac{(\mathrm{X} - \mu)^{2}}{2 \sigma^{2}}}}{\sqrt{2 \pi} \sigma} \mathrm{dX} 一般实际计算过程中,使用简单形式替换: 0.5 \mathrm{x}\left(1+\tanh \left[\sqrt{\frac{2}{\pi}}\left(\mathrm{x}+0.044715 \mathrm{x}^{3}\right)\right]\right) 或者使用: x \sigma(1.702x) 优点:
源码中的GELU 在google-research/bert/modeling.py中的GELU,也是采用近似的形式实现的: def gelu():cdf = 0.5 * (1.0 + tf.tanh((np.sqrt(2 / np.pi) * (x + 0.044715 * tf.pow(x, 3))))) return x * cdf 而在pretrained-BERT-pytorch/modeling.py中,更加精准: def gelu(x):"""Implementation of the gelu activation function. For information: OpenAI GPT's gelu is slightly different (and gives slightly different results): 0.5 * x * (1 + torch.tanh(math.sqrt(2 / math.pi) * (x + 0.044715 * torch.pow(x, 3)))) Also see https://arxiv.org/abs/1606.08415 """ return x * 0.5 * (1.0 + torch.erf(x / math.sqrt(2.0))) 7 小结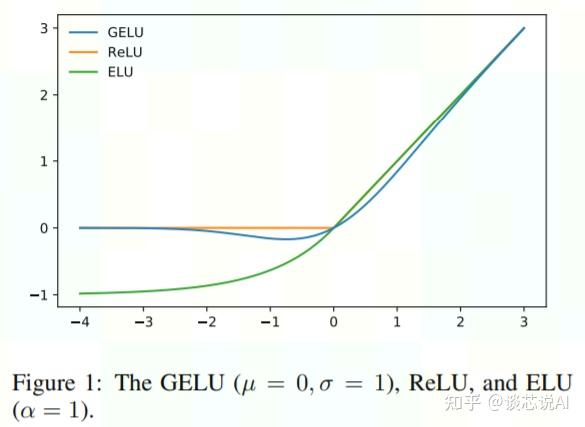 上图来源于论文:gaussian error linear units
5、全连接层全连接层(fully connected layers,FC)在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。之前MLP网络中使用的就是大量的全连接层组成的网络。 我们都知道全连接层是最需要参数支撑的(可占整个网络参数80%左右),对模型影响参数:
作用及使用方式: 最后一层FC一般用于分类,输出不同类的概率。 全连接层宽度或长度增加,神经元个数增加,模型复杂度提升。理论上可以提高模型的学习能力。长度和宽度都是越多越好?肯定不是,原因有:
替代方案:用全局平均池化(global average pooling,GAP)取代全连接层来融合学到的深度特征。如ResNet和GoogLeNet等。 同全连接层相比,GAP的一个优点
|