|
最近学习了拉格朗日乘数法(Lagrange multiplier),把自己的理解写下。 由于初学乍练,如有错误欢迎指正。 介绍在数学中的最优化问题中,拉格朗日乘数法(以数学家Joseph-Louis Lagrange命名)是一种寻找多元函数在其变量受到一个或多个条件的约束时的极值的方法。 这种方法可以将一个有n个变量与k个约束条件的最优化问题转换为一个解有n + k个变量的方程组的解的问题。这种方法中引入了一个或一组新的未知数,即拉格朗日乘数,又称拉格朗日乘子,或拉氏乘子,它们是在转换后的方程,即约束方程中作为梯度(gradient)的线性组合中各个向量的系数。
比如,要求 {\displaystyle f(x,y)} ,在 {\displaystyle g(x,y)=c\,} 时的最大值时,我们可以引入新变量拉格朗日乘数 \lambda ,这时我们只需要下列拉格朗日函数的极值:
{\displaystyle {\mathcal {L}}(x,y,\lambda )=f(x,y)+\lambda \cdot {\Big (}g(x,y)-c{\Big )}}
更一般地,对含n个变量和k个约束的情况,有:
{\displaystyle {\mathcal {L}}\left(x_{1},\ldots ,x_{n},\lambda _{1},\ldots ,\lambda _{k}\right)=f\left(x_{1},\ldots ,x_{n}\right)-\sum \limits _{i=1}^{k}{\lambda _{i}g_{i}\left(x_{1},\ldots ,x_{n}\right)},}
拉格朗日乘数法所得的极点会包含原问题的所有极值点,但并不保证每个极值点都是原问题的极值点。 几何解释设三维空间的曲面 z=f(x,y) ,在限制条件 g(x,y)=0 之下,求其极值。 如图所示,假设 z=f(x,y) 是一个抛物面,限制条件 g(x,y)=0是一个平面,它和 z=f(x,y) 相交得一个抛物线,问题等价于怎么算这个抛物线的极值?
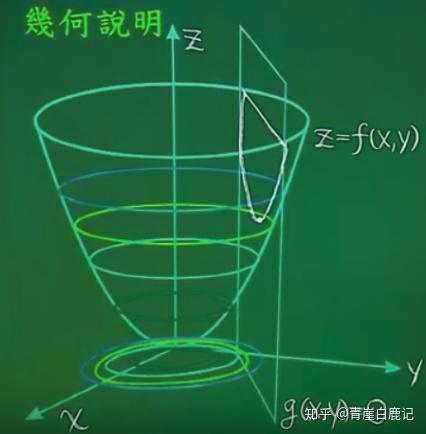
图1
先看等高线 f(x,y)=d_n ,如图2所示:

图2
想像此时我们移动 g(x,y)=0 上的点,因为 f 是连续的方程,我们因此能走到 f \left( x, y \right)=d_n 更高或更低的等高线上,也就是说 d_{n} 可以变大或变小。
只有当 g(x,y)=0 和 f \left( x, y \right)=d_n 相切,这种情况下,会出现极值或鞍点。
为什么必须相切?因为如图3所示:如果限制曲面在A处和一条等高线相交,必然与比A处低的等高线上的B点相切
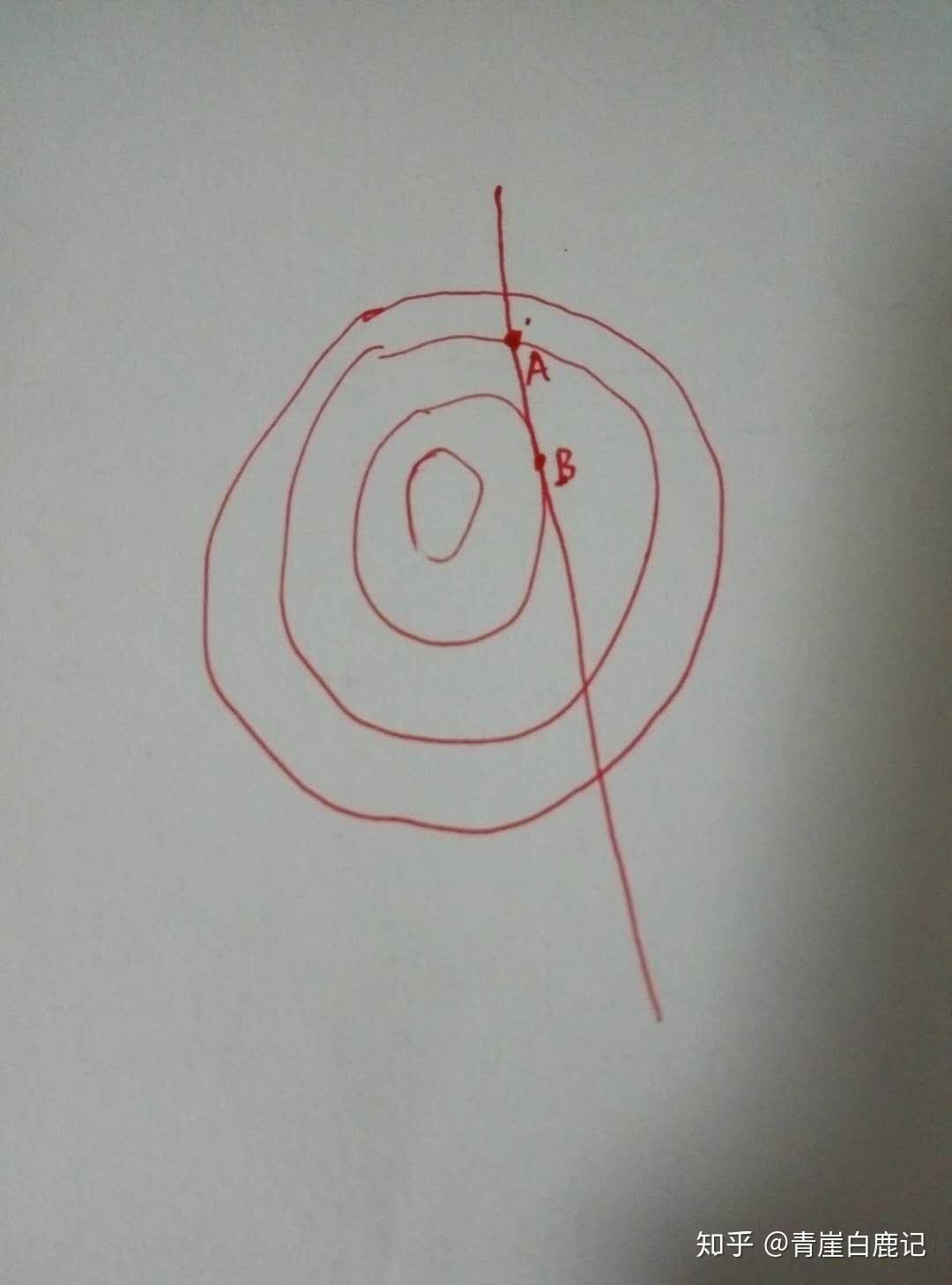
图3
现在证明在当 g(x,y)=0 和 f \left( x, y \right) 的等高线相切时: \nabla f=\lambda \nabla g

图5
设函数 f(x,y) 在 A点处有极值 \kappa ,且在A点的邻域内连续。则在A点处有 {\displaystyle f\left(x,y\right)=\kappa }
另有一常值函数 {\displaystyle g\left(x,y\right)=c}
两个函数在A点处的全微分为
{\displaystyle \mathrm {d} f={\frac {\partial {f}}{\partial {x}}}\mathrm {d} x+{\frac {\partial {f}}{\partial {y}}}\mathrm {d} y=0}
{\displaystyle \mathrm {d} g={\frac {\partial {g}}{\partial {x}}}\mathrm {d} x+{\frac {\partial {g}}{\partial {y}}}\mathrm {d} y=0}
由于 \mathrm{d}x 和 \mathrm{d}y 是任取的无穷小量,故该线性方程组的系数成比例,有
{\displaystyle {\dfrac {\dfrac {\partial {f}}{\partial {x}}}{\dfrac {\partial {g}}{\partial {x}}}}={\dfrac {\dfrac {\partial {f}}{\partial {y}}}{\dfrac {\partial {g}}{\partial {y}}}}=-\lambda }
即
{\displaystyle {\frac {\partial {f}}{\partial {x}}}+\lambda \cdot {\frac {\partial {g}}{\partial {x}}}=0}
{\displaystyle {\frac {\partial {f}}{\partial {y}}}+\lambda \cdot {\frac {\partial {g}}{\partial {y}}}=0}
将上二式分别乘以 \mathrm{d}x 和 \mathrm{d}y,再相加并积分,得到一新函数
{\displaystyle {\mathcal {L}}(x,y,\lambda )=f(x,y)+\lambda \cdot g(x,y)}
那么,求原函数极值的问题就转化为求该函数极值的问题。
类似地,这种求极值的方法也可以推广到多维函数
{\displaystyle f\left(x_{1},\ldots ,x_{n}\right)}
参考资料: [1] Lagrange multiplier [2] PRML [3] 中华科技大学数位课程 |



